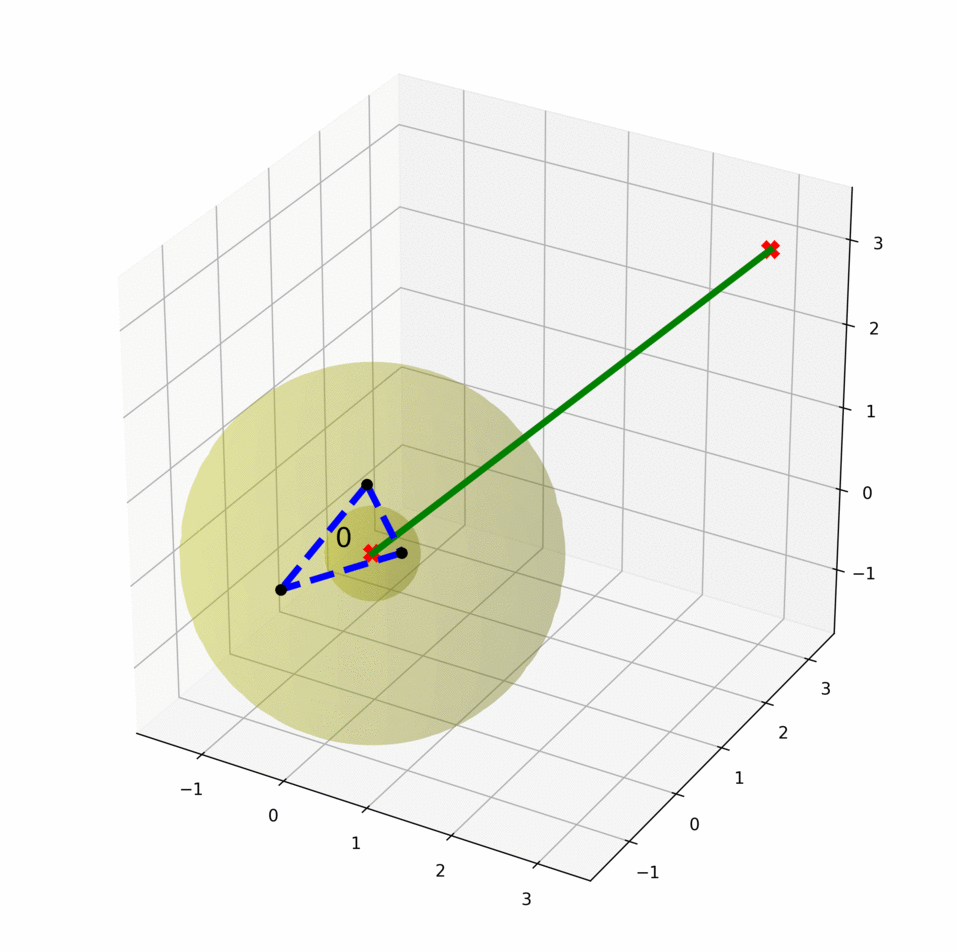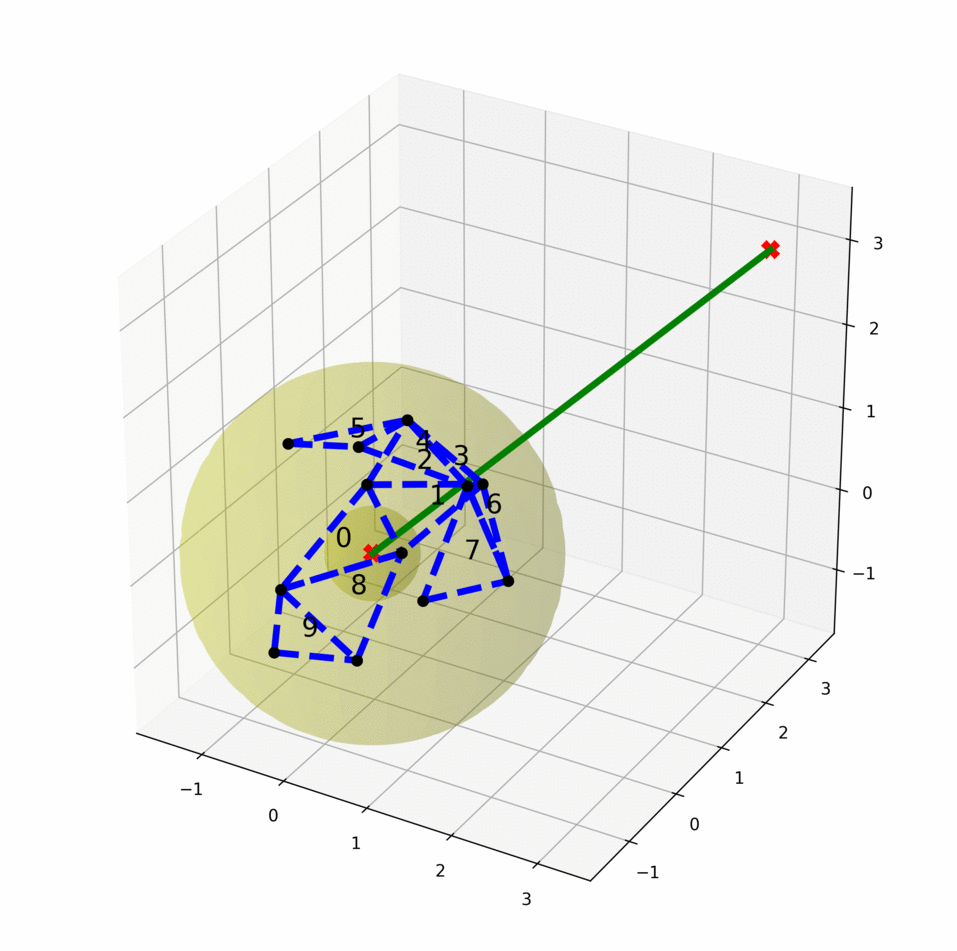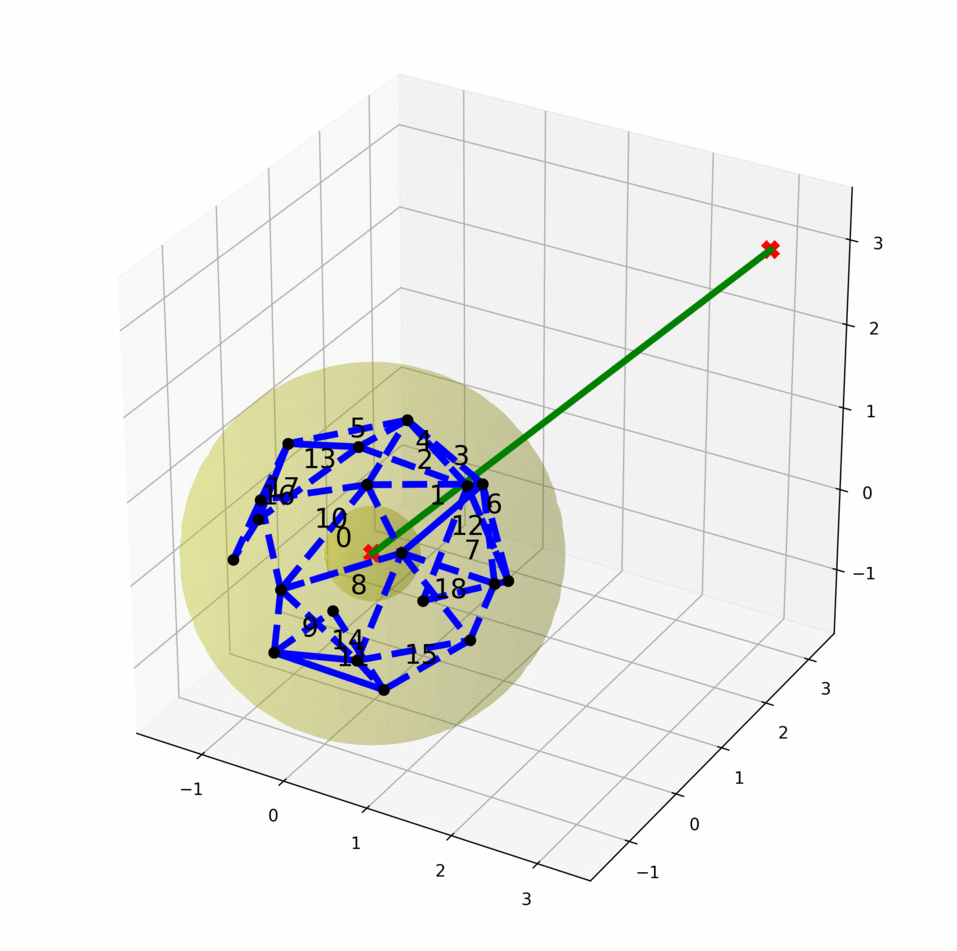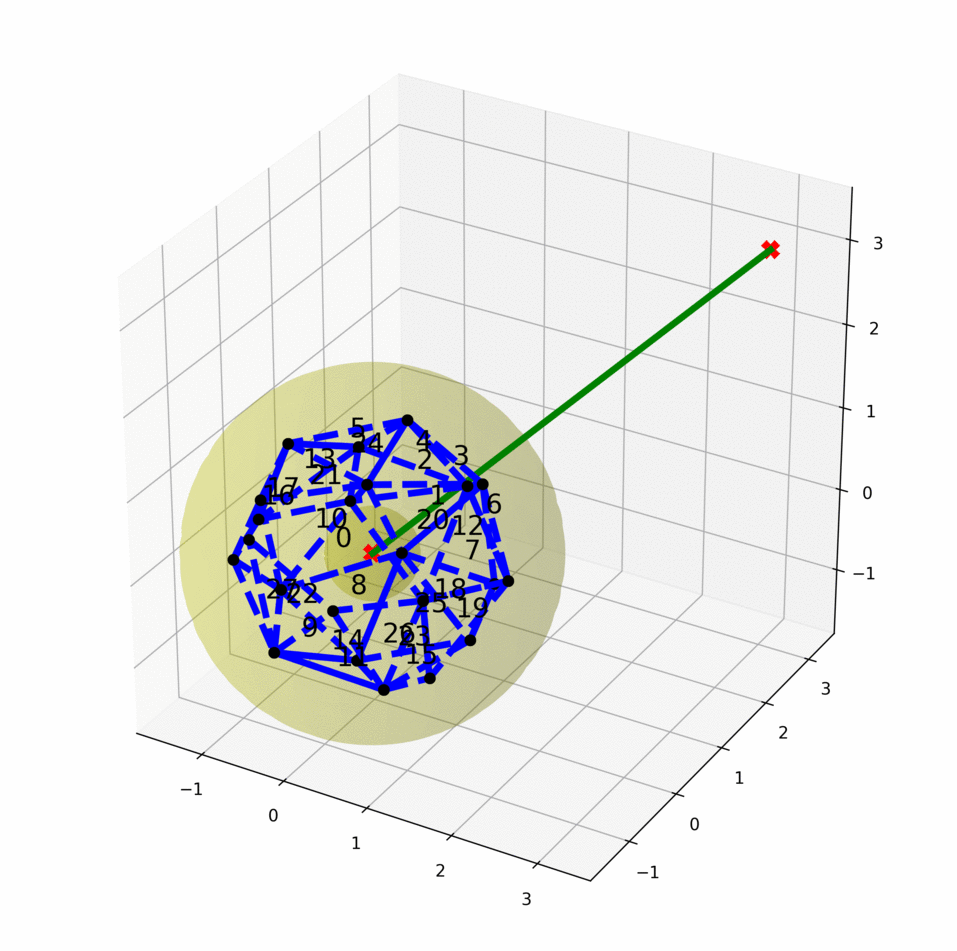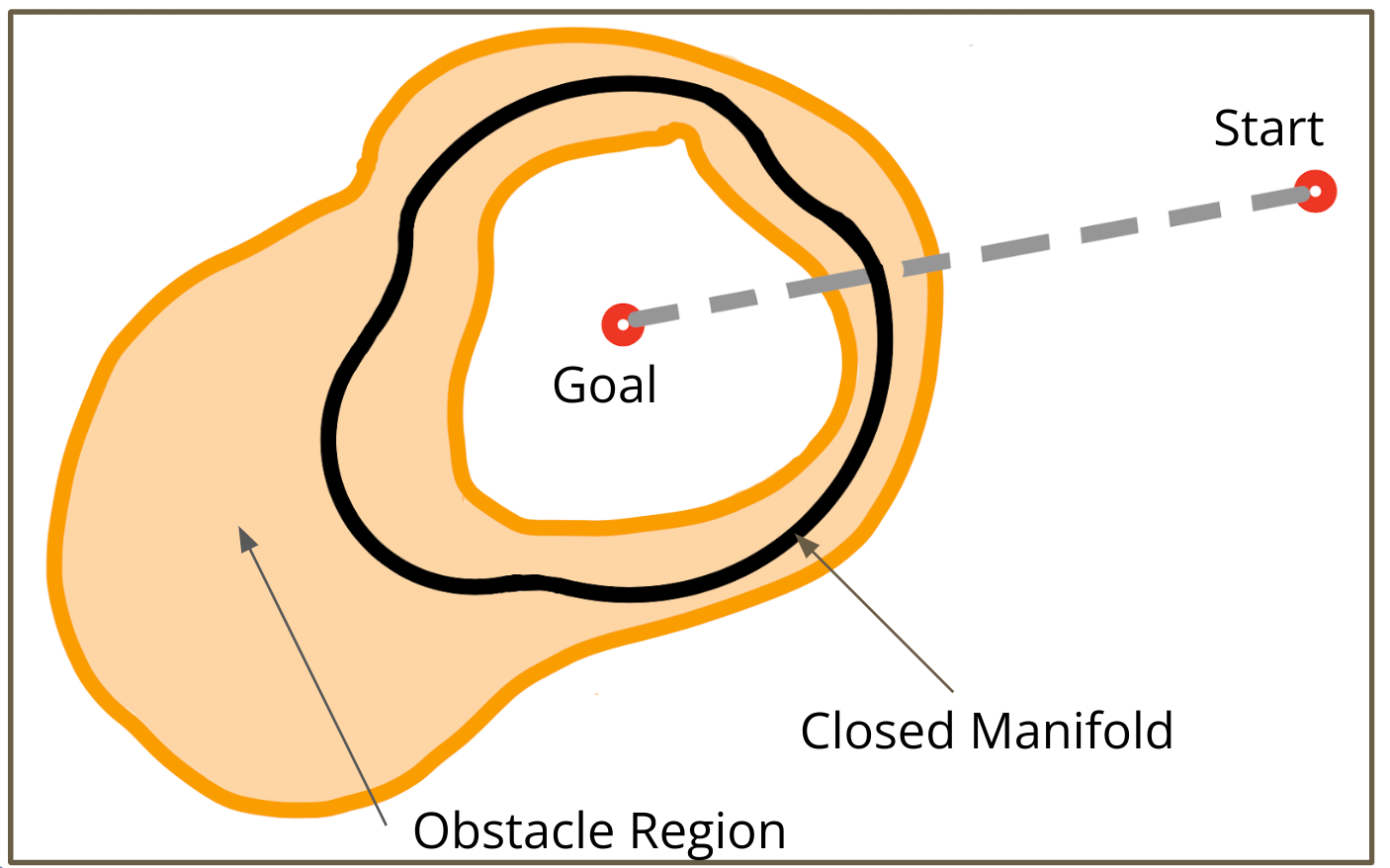

Sampling-based motion planners are effective in high-dimensional spaces but are only probabilistically complete. Consequently, these planners cannot provide a definite answer if no plan exists, which is important for high-level scenarios, such as task-motion planning. This work focus on finding infeasibility guarantees for kinematic motion planning problems. We define motion planning infeasibility proof as a manifold in the configuration space that exists entirely in the obstacle region of the configuration space and separates the start and the goal. Starting from our first algorithm that constructs infeasibility proofs in the configuration space directly, now we have developed a learning-based algorithm to generate infeasibility proofs more efficiently. This work is still in progress.



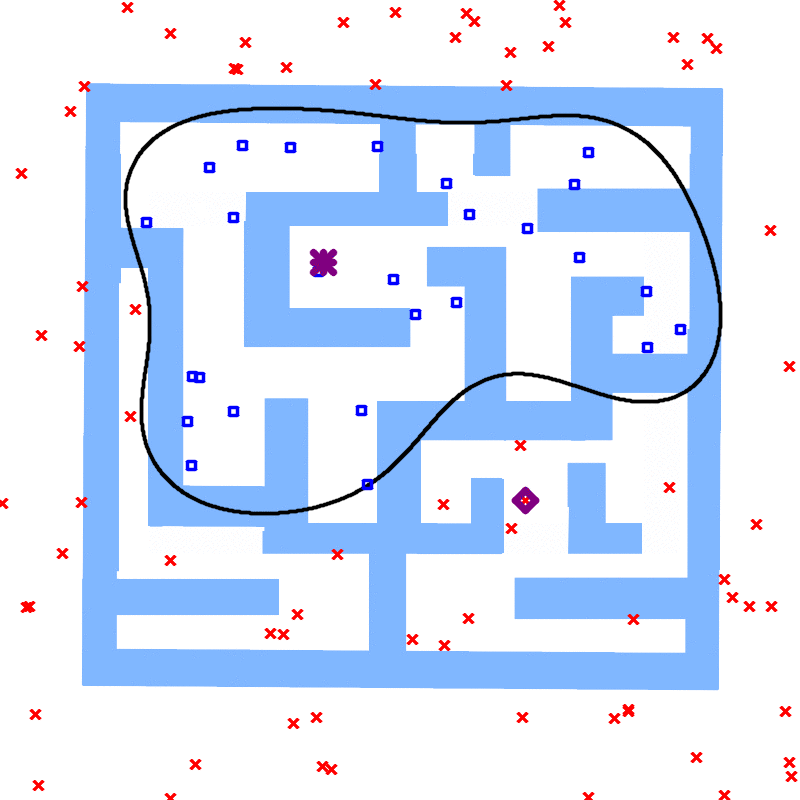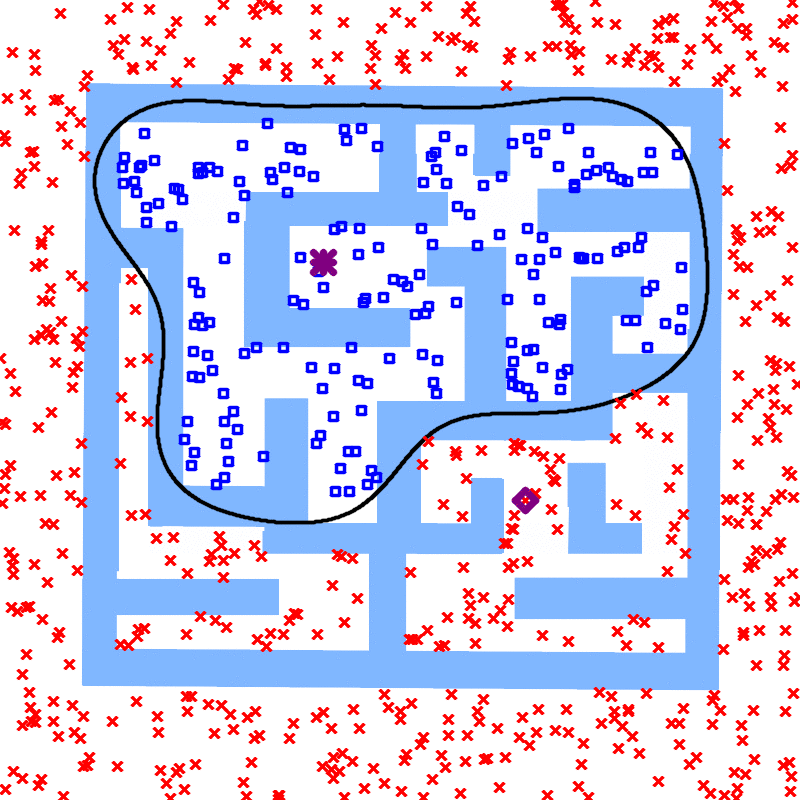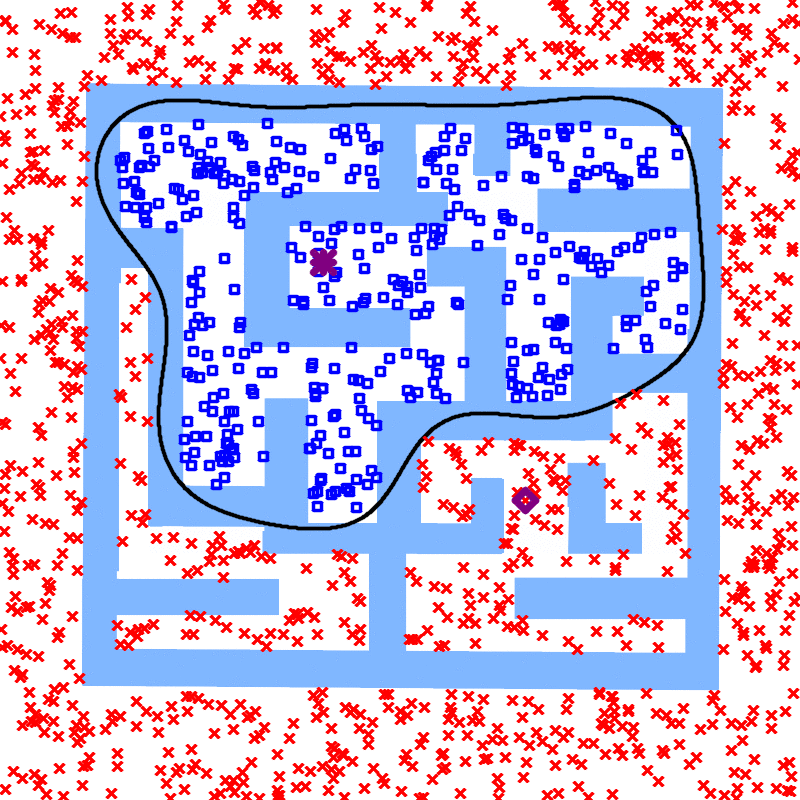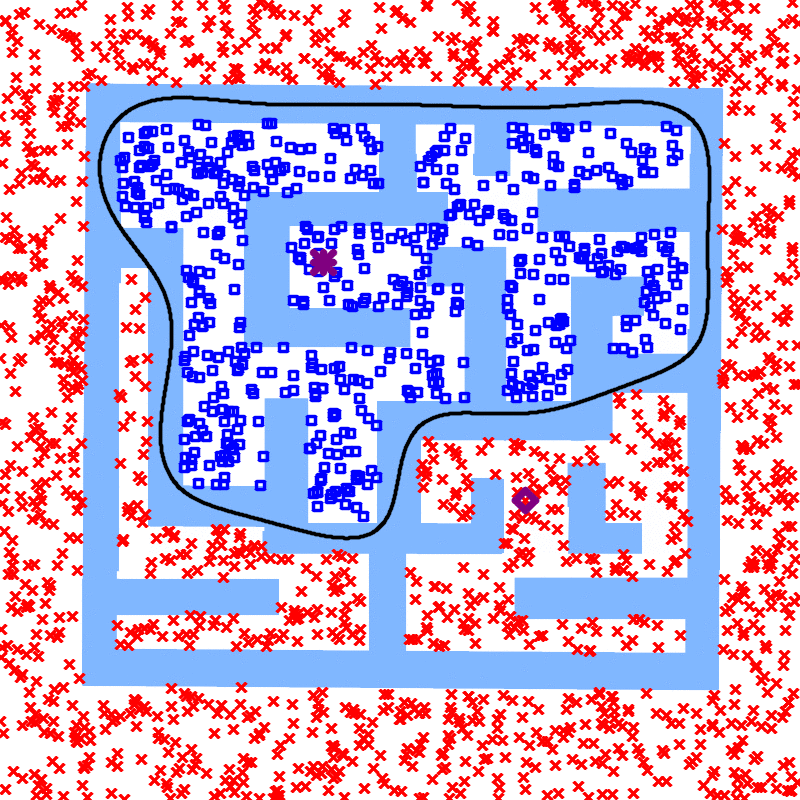
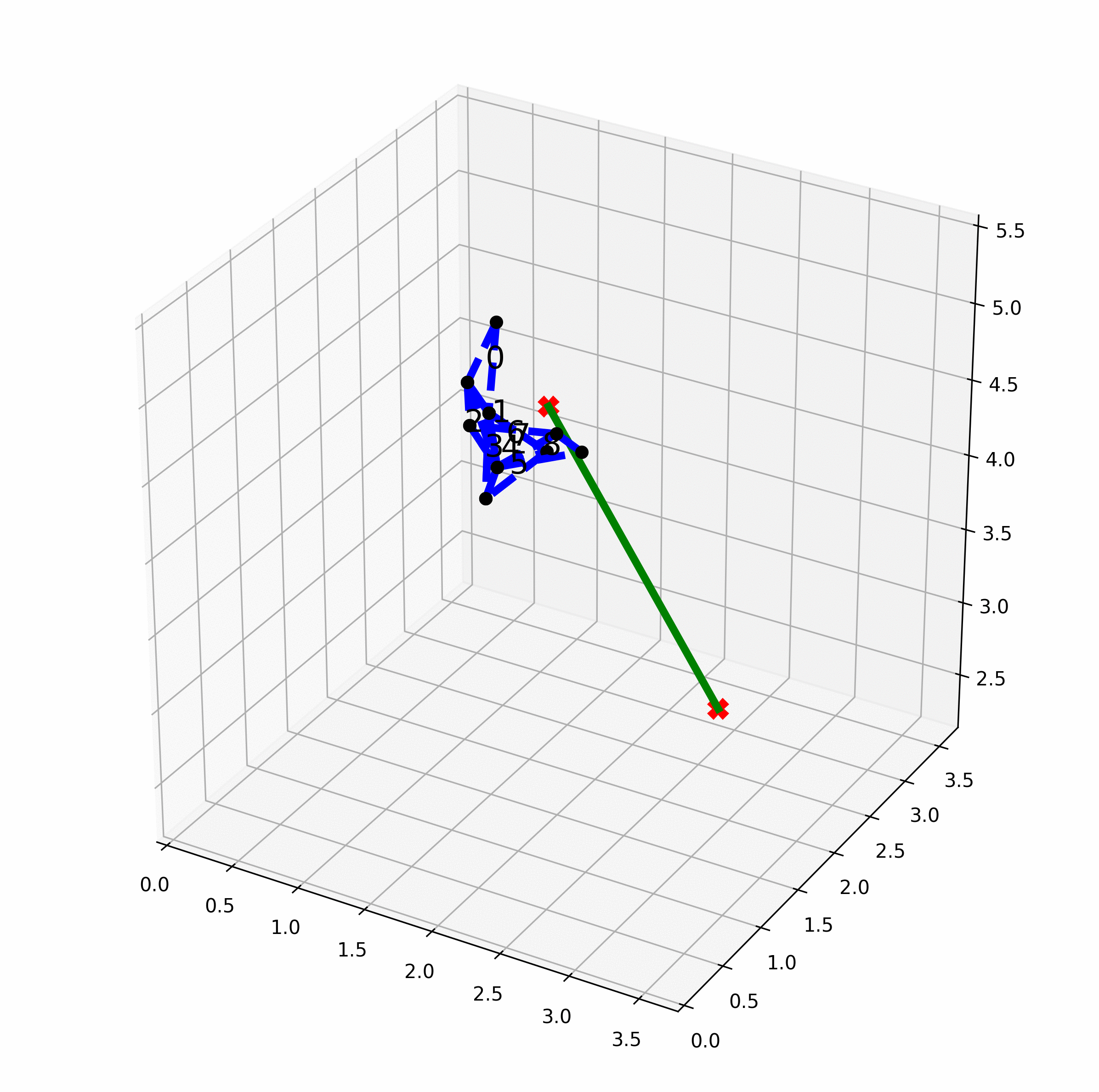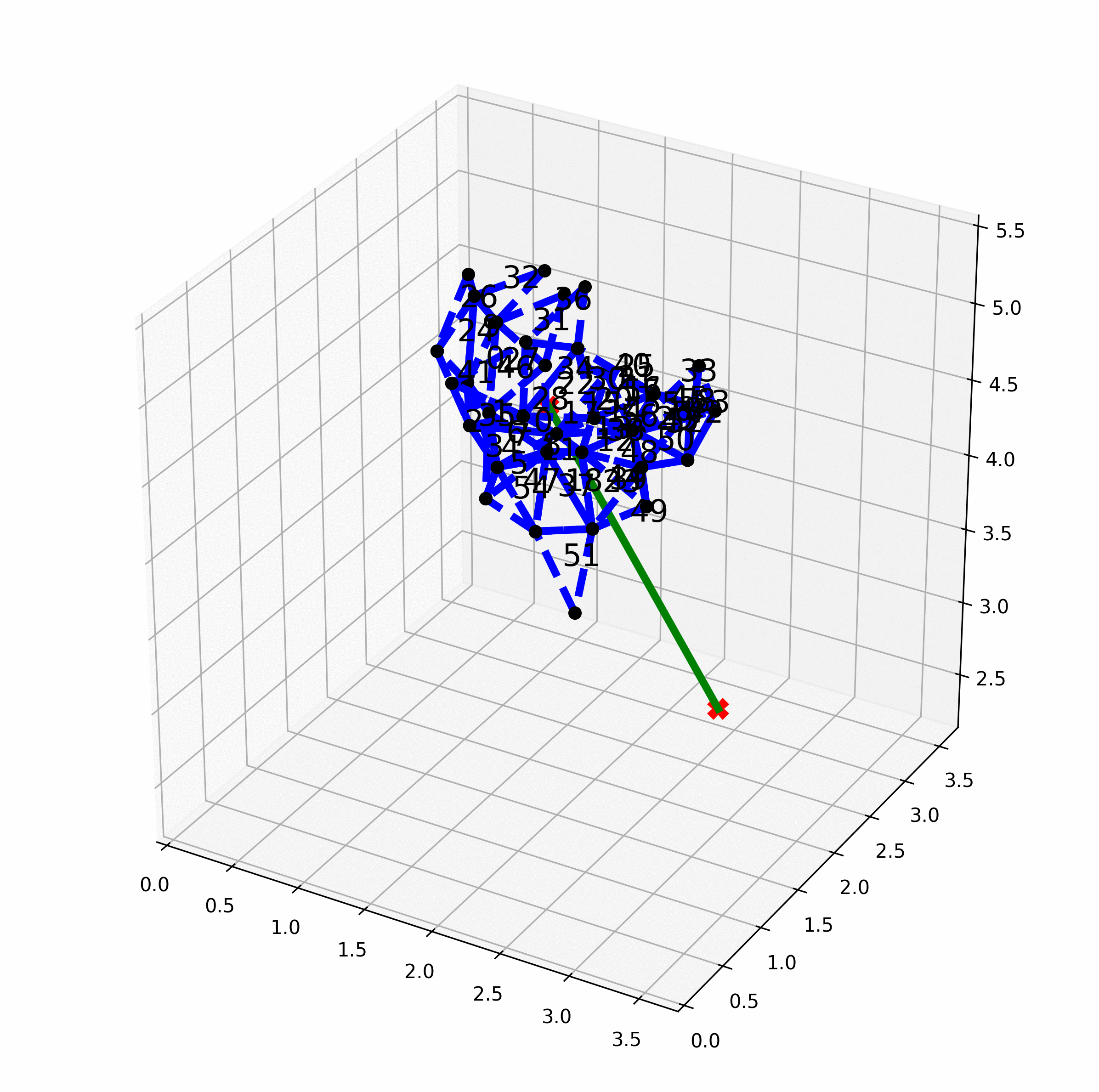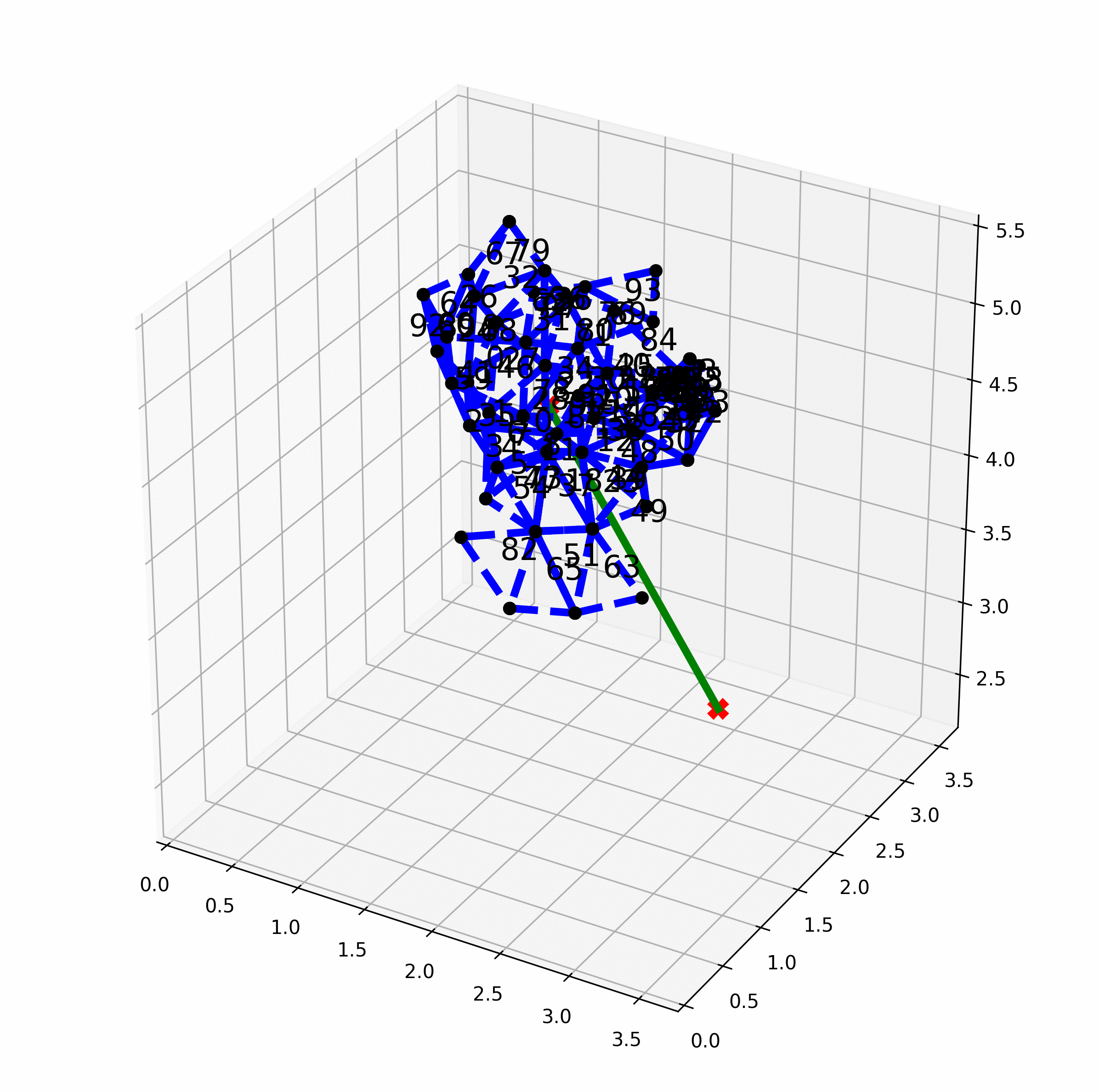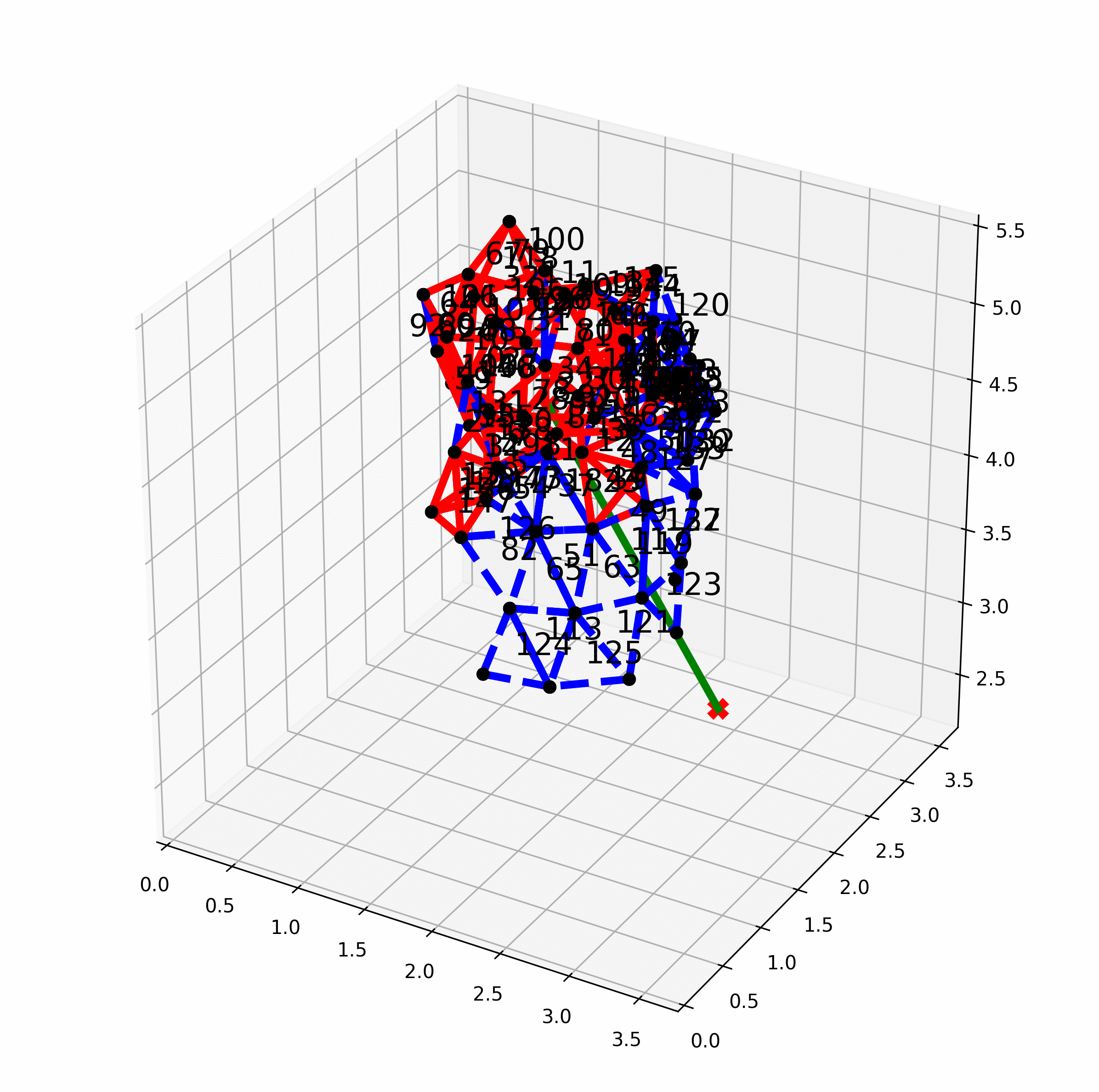
We treat the samples in the two search trees/graph components as two classes and learn a classifier. Geometrically, the classifier is a separating manifold for the two classes of samples. The learned manifold fits into the obstacle region as more points are sampled, and eventually becomes an infeasibility proof when the manifold is entirely in the obstacle region of the configuration space.
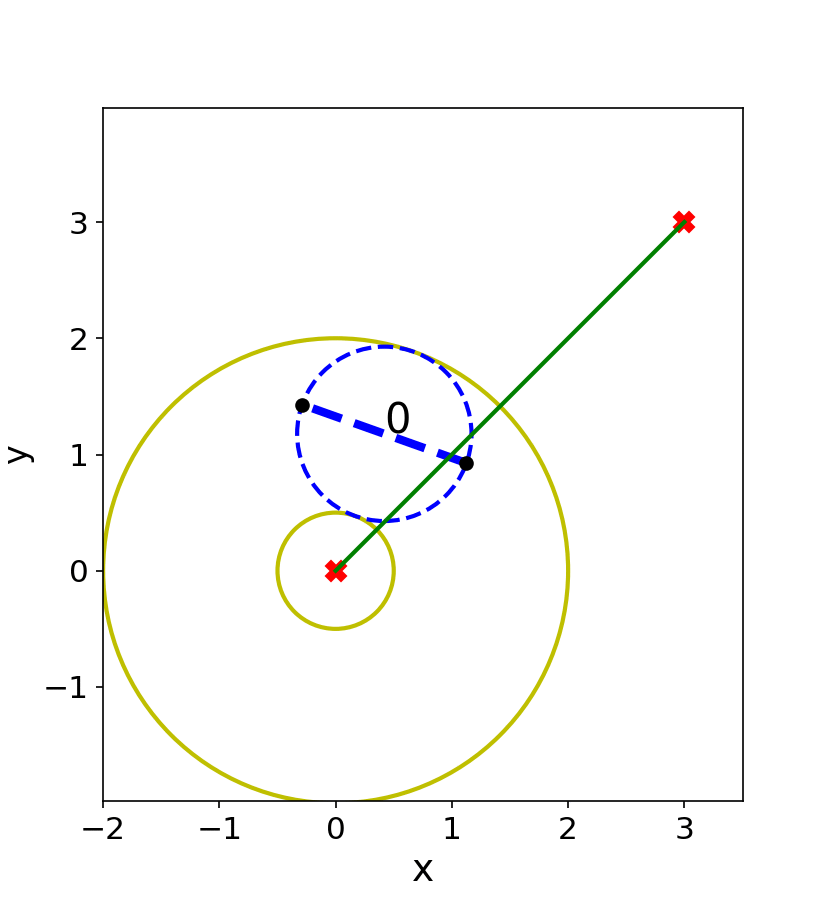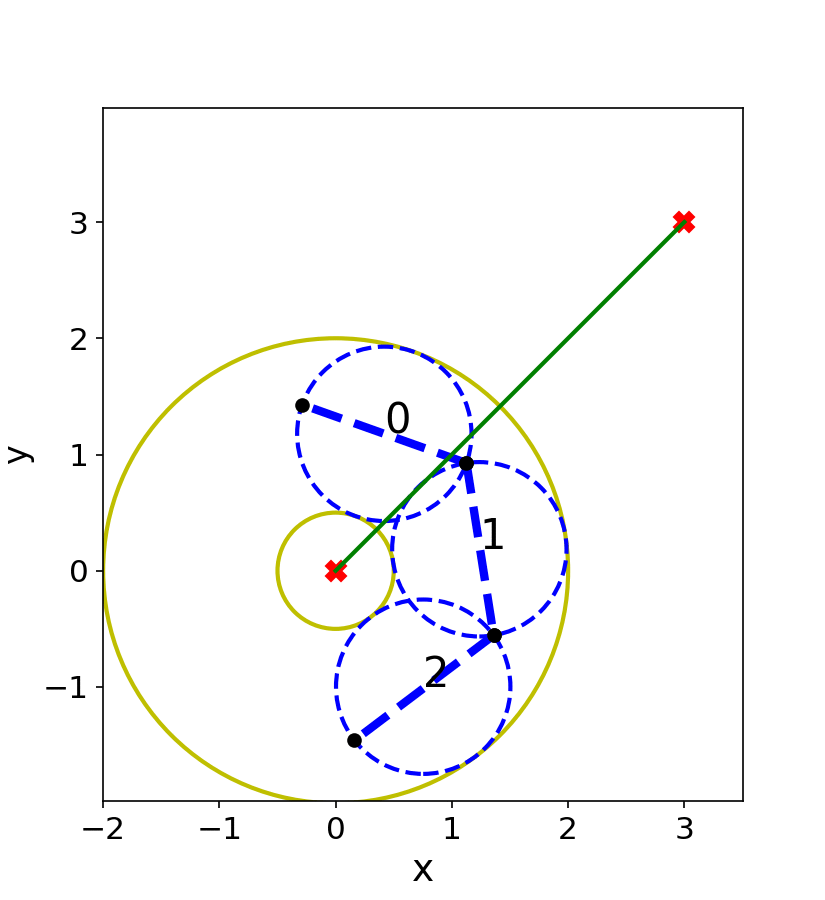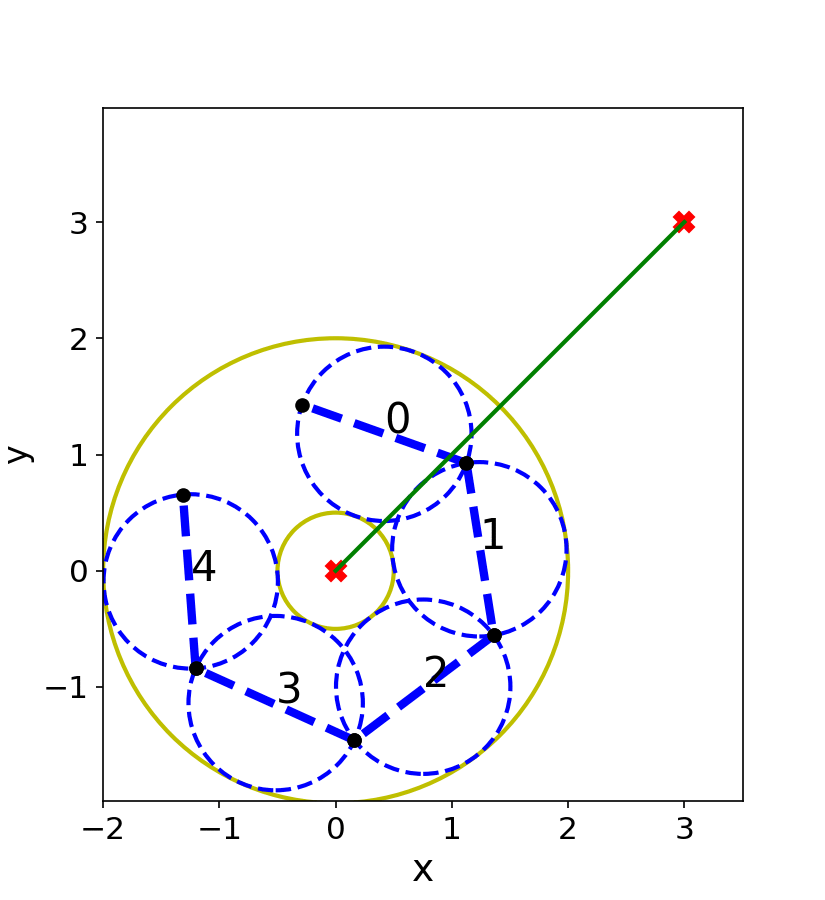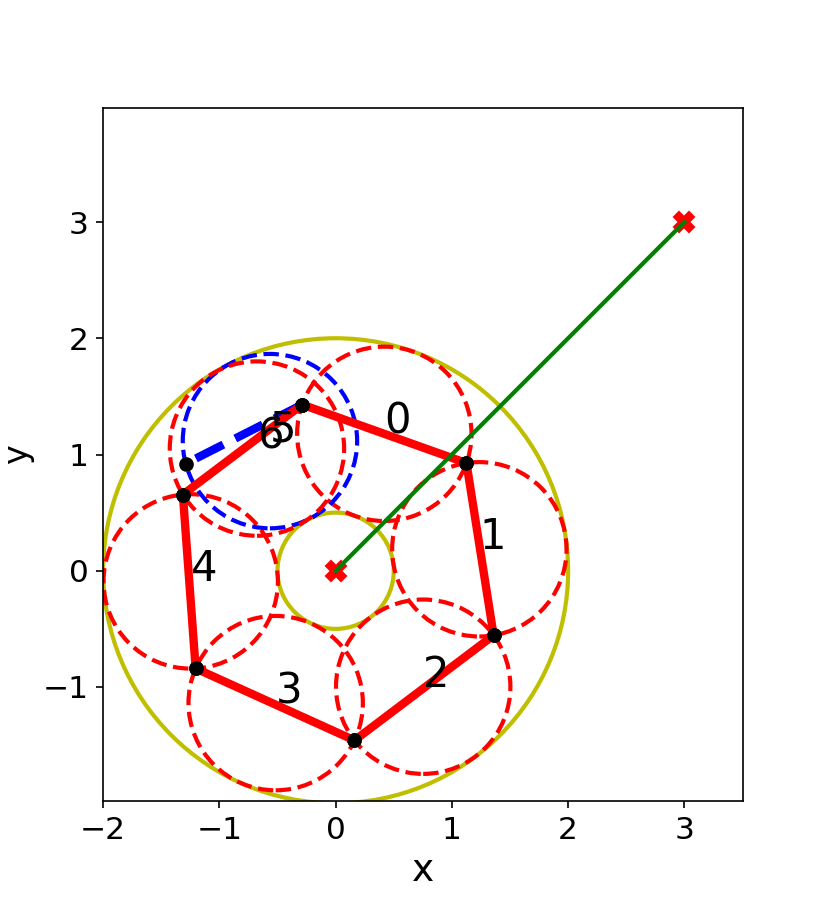
We have presented a general method for motion planning infeasibility proofs and demonstrated the approach on a low-dimensional manipulator. Our approach progressively grows volumes in the obstacle region via sampling and optimization and then attempts to find a closed polytope separating the start and goal via constraint solving.