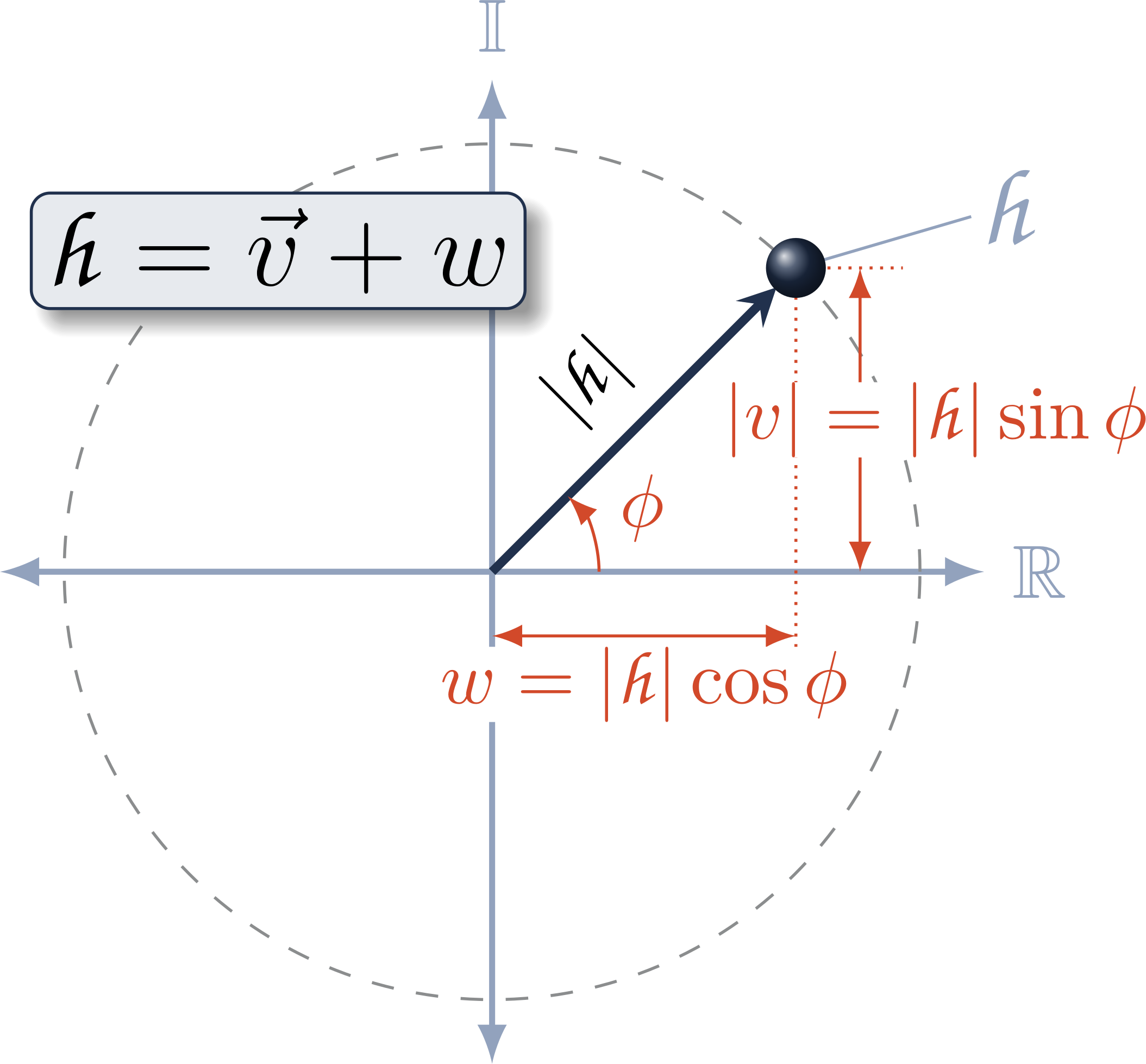

Modern approaches for robot kinematics employ the product of exponentials formulation, represented using homogeneous transformation matrices. The unit dual quaternions are an established alternative representation; however, their use presents certain challenges: the dual quaternion exponential and logarithm contain a zero-angle singularity, and many common operations are less efficient using dual quaternions than with matrices. We present a new derivation of the dual quaternion exponential and logarithm that removes the singularity, and we show that an implicit representation of dual quaternions is more efficient than transformation matrices for common kinematics operations. This work offers a practical connection between dual quaternions and modern exponential coordinates, demonstrating that a dual quaternion-based approach provides a more computationally-efficient alternative to matrix-based representations for many operations in robot kinematics.


We present a method for Cartesian workspace control of a robot manipulator that enforces joint-level acceleration, velocity, and position constraints using linear optimization. This method is robust to kinematic singularities. On redundant manipulators, we avoid poor configurations near joint limits by including a maximum permissible velocity term to center each joint within its limits. Compared to the baseline Jacobian damped least-squares method of workspace control, this new approach honors kinematic limits, ensuring physically realizable control inputs and providing smoother motion of the robot
We generate workspace trajectories for multiple waypoints, such that each trajectory segment has constant-axis rotation. This improves on the "textbook" approaches which are point-to-point, e.g., SLERP, or take indirect paths, e.g. axis-angle blends. We derive this approach by blending subsequent spherical linear interpolation phases, computing interpolation parameters so that rotational velocity is continuous.
We show that accurate, visually-guided manipulation is possible without static camera registration. Here, we register the camera online, converging in seconds, by visually tracking features on the robot and filtering the result. This handles cases such as perturbed camera positions, wear and tear on camera mounts, and even a camera held by a human.

